Under Construction 
Stress is defined as the force per unit area. Thus, the formula for calculating stress is:
F
σ = –
A
Where σ denotes stress, F is load and A is the cross sectional area. The most commonly used units for stress are the SI units, or Pascals (Pa = N/m2) Newtons per Square meter, although other units like psi (pounds per square inch) are sometimes used.
Elastic materials stretch (elongate) in proportion to force up to a point.
Stress is the force applied to the specimen and,
Strain is the relative elongation of the specimen from its original length.
Breaking Point & Elongation
A - This is a feature of system take-up.
At very low forces, elongation is not linear.
B - This is the linear portion of the stress/strain curve.
It conforms to Hooke's law (F = kΔL)
C - This is the limit of proportionality, (LOP), where linearity gives way
to nonlinear behaviour.
D - This is called the yield point, or yield strength
a.k.a. the elastic limit. This point marks the end of the elastic region
and the start of the plastic region, within which no extra force is required
to further extend the sample. If the test is terminated within this region,
the sample will not return to its original dimensions.
The end of the plastic region is marked by point E,
after which extra force is required to extend the sample further.
F - This is known as the ultimate strength of the material, after which sample break (point G) occurs.
See Bolts and screws here
and Climbing Ropes
Compressive Strength: Ceramics typically have good tensile strengths and are used under compression e.g. concrete.
Ceramics typically have good tensile strengths and are used under compression e.g. concrete.When I was taking introductory engineering we made concrete blocks then crushed them with a testing machine. The strength of the blocks varied depending on the amount of water in the mixture. The time and temperature of curing also affects strength. Shear Strength: 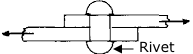 Shear | Strength of Materials Virtual Laboratory
A Moment of a Force The stronger the force, and the greater the distance at which it acts, the larger the moment or "turning force" it will produce.
A moment or "turning force" (M) is calculated by multiplying a force (F) by its moment arm (d). The moment arm is the distance at which the force is applied, taken from the fixed point:
Beam or Bending Moment:
Yield Strength:
Links: |